难题是高冷孤傲的美女,她戴着层层面纱,穿着厚厚伪装,若你能卸下她的所有遮挡,就会看到那亲切可爱的熟悉面容……
本期文章在前面基础上分析较难的动点轨迹与路径最值结合的综合性问题,常规问题和基本模型请参阅前期相关文章,文后有链接。

乾坤倒转

例1.如图,点A是直线y=-x上的动点,点B是x轴上的动点,在矩形ABCD中,AB=2,AD=1,则OD的最大值为 。
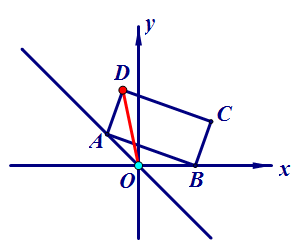
解析:本题从常规方法看,应寻找D点轨迹,但这里似乎不好确定D的运动轨迹是哪种图形。
由题意知∠AOB=45°或135°,AB=2,为定线对定角基本图形,所以O点在以AB为弦的圆弧上。考虑到点D与矩形及AOB外接圆的相对位置不变,所以我们换一个角度,让圆和矩形不动,则O点是圆P上的动点,也即点O的运动路径是圆P,从而OD即为定点D到圆P的路径。
如上图,易知点心距PD=1,圆P的半径为√2,所以OD的最小值为√2-1,最大值为√2+1。
本题也可以从三角形三边关系判断,如下图,OP+PD≤OD≤OP-PD,但仍需先判断OP为定值,即AOB共圆,且OPD三点可能共线。

若题目关键点中的动点较多,定点较少,可以根据运动的相对性,把动的部分静止,就相当于把定的部分运动,来一个乾坤倒转,问题就很清楚明了。


主从联动

例2.如图,已知点A(3,0),C(0,-4),⊙C的半径为√5,点P为⊙C上一动点.连接AP,若M为AP的中点,连接OM,则OM的最大值= 。
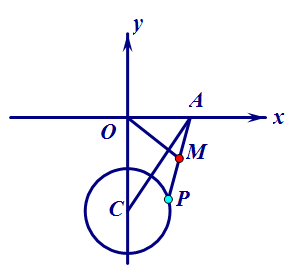
分析:此题中的O点是定点,M点是动点,显然要先确定动点M的运动轨迹是什么图形。从条件看,M点随P点运动,且与定点A的距离比为定值AM:AP=1:2,符合主从联动型问题,得M点运动轨迹为以AC中点为圆心,以圆C半径的1/2为半径的圆。
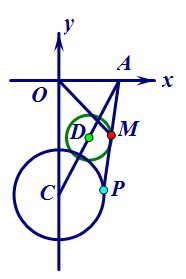
如上图,转化为定点O到定圆D的最短路径,得最大值为5/2+√5/2,最小值为5/2-√5/2。
另外,本题也可以根据中点条件构造OQ=AO得中位线OM=1/2PQ,转化为求PQ的最小值,仍然是求定点Q到定圆C的最短路径问题,其本质并无不同。

主从联动的动点轨迹问题已有前文论述,参考阅读:探本求源-秒解旋转缩放型的动点路径问题


观木见林

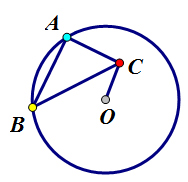
例3.已知⊙O半径为3,点A、B在⊙O上,∠BAC=90°,AB=AC,求OC的最小值。
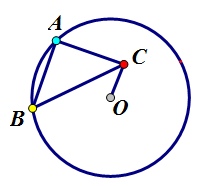
分析:本题中点A、B都是圆O上的动点,若要完整地画出C点轨迹,可能不太容易。首先看用电脑画出A、B两点双动时C点的轨迹,如下图。
可见,点C的轨迹应是一个封闭的圆环。但是不用几何画板这样工具的话,好像不容易看到这个圆环。
怎么办呢?当然有办法,可以按照下面的方法解决。
(1)若点A不动,点B在圆O上运动一周,则点C是由动点B绕定点A逆时针旋转90°而来,点B是主动点,点C是从动点,所以此时点C的运动轨迹也是由点B的运动轨迹绕点A逆时针旋转90°而得,即⊙O绕点A逆时针旋转90°就是点C的轨迹,如下图。[原理参阅:探本求源-秒解旋转缩放型的动点路径问题,也有老师形象总结为“瓜豆原理”]
再把点A在圆O上运动一周,这时红色轨迹圆也随之绕点O运动一周,如下图。
上图的的红色区域就是完整的C点轨迹,它是点A、B在圆周上随机运动时C点所有可能的位置。
由上图可知,P点的完整轨迹是红色圆环,转化为求定点O到红色圆环的最短路径,得内圆半径3√2-3即为OC的最小值,外圆半径3√2+3即为OD的最大值。
当然,为简单起见,如下图,我们让A点静止在某处不动,C点随B点运动一周形成的轨迹是圆D,此时转化为定点O到定圆D的最短路径,可以得出同样的结果。为什么可以用这一种位置代替上图中整个圆环?因为点A与圆心O的距离不变,无论点A运动到何处,点O到C点所在轨迹的相对距离都相同。即可以让点A不动代替点A运动一周的所有情况,上图的点O到圆环与下图的点O到圆D的最短(长)路径结果是一样的。(此处有点烧脑,需从动态视角和全局视角考虑)

(2)若点B不动,点A在圆O上运动一周,则点C是由动点A绕定点B逆时针旋转90°且放大√2倍(因CB:AB=√2:1)而来,点A是主动点,点C是从动点,所以此时点C的运动轨迹也是由点A的运动轨迹绕点B逆时针旋转90°且放大√2倍而得,即⊙O绕点A逆时针旋转90°且放大√2倍就是点C的轨迹,如下图。
此时轨迹圆心D同样是点O绕点B逆时针旋转90°且放大√2倍而得,如下图,转化为求定点O到定圆D的最短(长)路径问题。
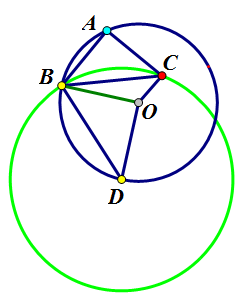
若再把B点也运动一周,下图的绿色轨迹圆也随之绕点O旋转一周所形成绿色圆环就是C点的全部轨迹,同(1)中红色圆环完全一样。可见用不同方法可以得到完全和谐一致的结果!
(3)若嫌上面的方法不好理解,也可以换个角度思考:
把ΔACO绕点A顺时值旋转90°得ΔABD,看出这样有什么好处吗?
CO转化为BD,并且BD在ΔBOD中,最关键的是BO、DO为定值,由三边关系易得:DO-BO≤BD≤DO+BO。此种方法的巧妙在于通过旋转得到一个大小确定的等腰直角三角形ADO,从而为解题带来方便。

上图本质上还是转化为圆到圆的最短路径,如下图,DO=3√2,所以点D在以O为圆心3√2为半径的圆上,而点B在以O为圆心3为半径的圆上,BD即为两个同心圆之间的路径,最小值为3√2-3,最大值为3√2+3。
本题中A、B两点双动时C点轨迹是下图中绿色圆环,实际解题时只要动其中一点即可。如下图的红色圆P,实质是从整个圆环轨迹中取一个圆,此时的情形可以代表整个圆环所有的情形,也即“观木见林”、“管中窥豹”,但首先心中要有“森林”、有“全豹”,否则便只知其然,不知其所以然。
如何理解动点和它的轨迹的关系?也许下面的几个比喻有所帮助。
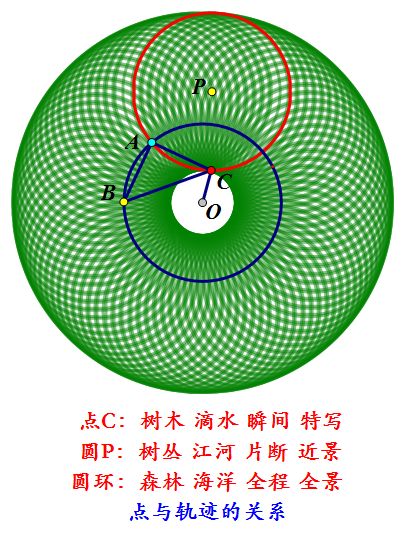
真是:动静辨分明,虽然你走我行各有路径,却是相牵相伴命中注定;点动有轨迹,犹如一片树木接连成林,恰似一捧珍珠互串成链。
突然发现,数学离诗歌很近,离哲学也很近!
有的解题者只用下面的图形利用三角形三边关系也可以算出答案,但是思考深度不够,所见范围较窄,属于“只见树木,不见森林”,不利于对轨迹的透彻理解,最好先判断全部轨迹再做简化处理。

例3还可以从旋转构造的角度产生多种解法,详见高阶思维之全局视角一文。
读者若有兴趣再试解一道变式题:
已知⊙O半径为3,点A、B在⊙O上,∠BAC=90°,AB:AC=4:3,求OC的最小值.