中考数学冲刺复习锐角三角函数的实际应用
中考数学冲刺复习
锐角三角函数
实际应用
【知识储备】包含视角（仰角、俯角）、方位角、坡度等题型。
1.如图1所示是一种太阳能路灯，它由灯杆和灯管支架两部分构成．如图2,AB是灯杆，CD是灯管支架，灯管支架CD与灯杆间的夹角∠BDC=60°,综合实践小组的同学想知道灯管支架CD的长度，他们在地面的点E处测得灯管支架底部D的仰角为60°,在点F处测得灯管支架顶部C的仰角为30°,测得AE=3m,EF=9m (A,E,F在同一条直线上），请解答下列问题：
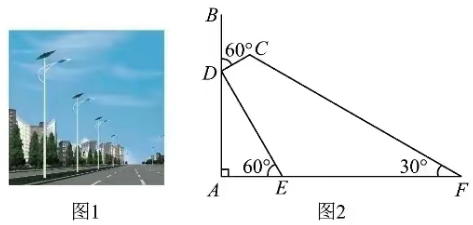
（1)求灯管支架底部距地面高度AD的长（结果保留根号）；
（2)求灯管支架CD的长度（结果精确到0. 1m,参考数据：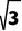
≈1. 73).
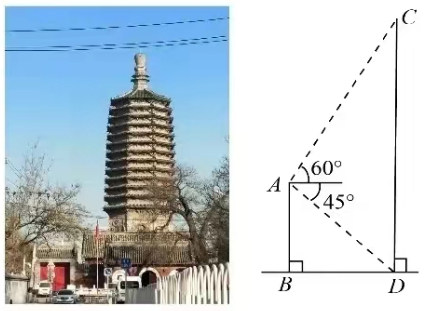
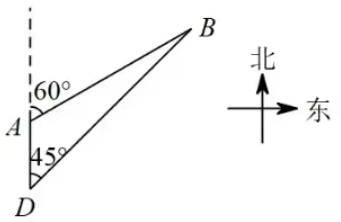
2.常州天宁寺始建于唐贞观年间，是佛教音乐梵呗的发源地之一，也是常州最大的寺庙，某校数学兴趣小组的同学利用卷尺和自制的测角仪尝试求解天宁寺宝塔的高度。如图所示，平地上一幢建筑物AB与宝塔CD相距56m,在建筑物的顶部分别观测宝塔底部的俯角为45°、宝塔顶部的仰角为60°.求天宁寺宝塔的高度（结果保留根号）．
数学陈老师:
3.如图，在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为i=1:2.4的斜坡AP攀行了26米到达点A,在坡顶A处又测得该塔的塔顶B的仰角为76°.
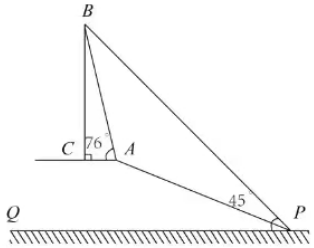
（1)求坡顶A到地面PQ的距离；
（2)计算古塔BC的高度（结果精确到1米）．（参考数据：sin76°≈0.97,cos76°≈0.24,tan76°≈4)
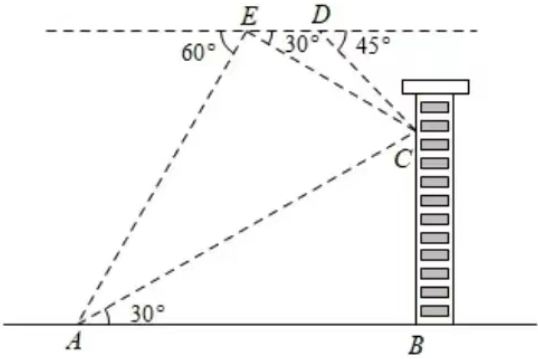
4.某地为庆祝元旦来临，在银杏广场举行无人机表演，点D、E处各有一架无人机，它们在同一水平线上，与地面AB的距离为60m.此时，点E到点A处的俯角为60°,点E到点C处的俯角为30°,点D到点C处的俯角为45°,点A到点C处的仰角为30°.求两架无人机之间的距离DE的长。
数学陈老师:
5.如图是某区域的平面示意图，码头A在观测站B的正东方向，码头A的北偏西60°方向上有一小岛C,小岛C在观测站B的北偏西15°方向上，码头A到小岛C的距离AC为10(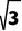+1)海里．
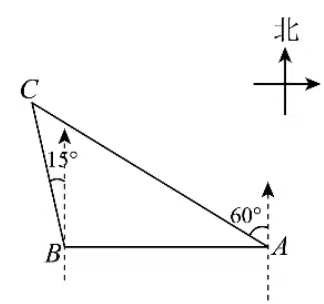
（1)∠BAC= _度，∠C= _度；
（2)求观测站B到AC的距离．
6.如图，某渔船向正东方向以14海里／时的速度航行，在A处测得小岛C在北偏东70°方向，2小时后渔船到达B处，测得小岛C在北偏东45°方向，已知该岛周围20海里范围内有暗礁．（参考数据：sin70°≈0.94,cos70°≈0.34,tan70°≈2.75, 2≈1.41)
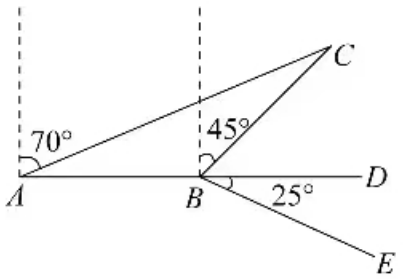
（1)求B处距离小岛C的距离（求出准确值）；
（2)为安全起见，渔船在B处向东偏南转了25°继续航行，通过计算说明船是否安全？
数学陈老师:
7.为了丰富学生社会实践活动，学校组织学生到红色文化基地A和人工智能科技馆C参观学习．如图，学校在点B处，A位于学校的东北方向，C位于学校南偏东30°方向，C在A的南偏西15°方向（30+30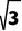)km处．学生分成两组，第一组前往A地，第二组前往C地，两组同学同时从学校出发，第一组乘客车，速度是40km/h,第二组乘公交车，速度是30km/h.哪组同学先到达目的地？请说明理由。
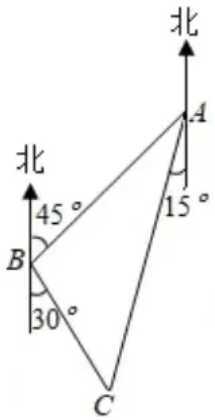
8.活动小组的同学为了测量某棵大树与建筑物间的距离，在大树A处测得建筑物B位于北偏东60°,他们向南走50m到达D点，测得建筑物B位于北偏东45°.求大树与建筑物之间的距离AB的长（参考数据：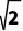
≈1.41, 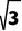≈1.732,结果精确到1m).
数学陈老师:
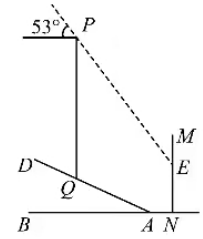
9.某居民楼MN后有一个坡度为i=1:2.4的小山坡，小区物业准备在小山坡上加装一广告牌PQ(如图所示），已知QA=5.2米，水平地面上居民楼MN距坡底A点的距离AN=1.2米．当太阳光线与水平线成53°角时，测得广告牌PQ落在居民楼上的影子EN长为3米，求广告牌PQ的高．（参考数据：sin53°≈4/5,cos53°≈3/5，tan53°≈4/3）
10.建筑物MN一侧有一斜坡AC,在斜坡坡脚A处测得建筑物顶部N的仰角为60°,当太阳光线与水平线夹角成45°时，建筑物MN的影子的一部分在水平地面上MA处，另一部分影子落在斜坡上AP处，已知点P的距水平地面AB的高度PD=5米，斜坡AC的坡度为1/3（即tan∠PAD=1/3），且M,A,D,B在同一条直线上。（测倾器的高度忽略不计，结果保留根号）
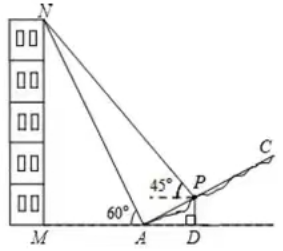
（1)求此时建筑物MN落在斜坡上的影子AP的长；
（2)求建筑物MN的高度．
数学陈老师:
11.如图，在距某居民楼AB楼底B点左侧水平距离60m的C点处有一个山坡，山坡CD的坡度（或坡比）i＝1:0.75,山坡坡底C点到坡顶D点的距离CD=45m,在坡顶D点处测得居民楼楼顶A点的仰角为28°,居民楼AB与山坡CD的剖面在同一平面内，求居民楼AB的高度（精准到0. 1m,参考数据：sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
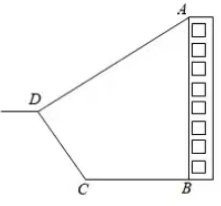
12.如图，某大楼的顶部树有一块广告牌CD,李明在山坡的坡脚A处测得广告牌底部D的仰角为53°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1: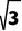,AB＝12米，AE=24米．（测角器的高度忽略不计，结果精确到0.1米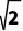，=1.414, 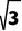=1.732,sin53°≈4/5,cos53°=3/5,tan53°≈4/3)
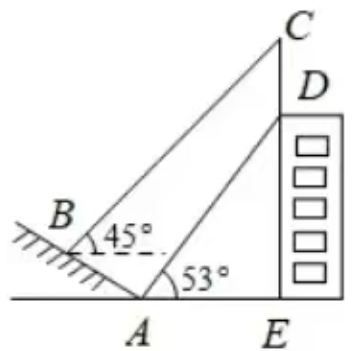
（1)求点B距水平地面AE的高度；
（2)求广告牌CD的高度．
13.如图，某防洪大坝的横截面是梯形ABCD,迎水坡CD的坡角为30°,坝顶AD宽度为2米，坝高AE为4米，背水坡AB的坡度i=1:1.
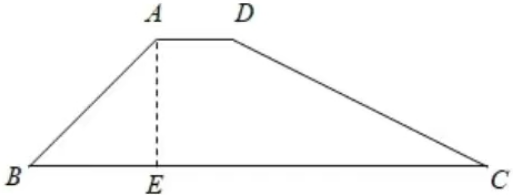
（1)求该堤坝的横截面积（结果保留根号）；
（2)为更好应对可能来临的汛情，防洪指挥部决定加固堤坝，要求坝高不变，坝顶宽度增加1米，背水坡的坡度改为i=1:1.5,求加固后的堤坝的横截面积（结果保留根号）．
【答案】
【分析】创作不易
【详解】赞赏后有解析过程
点赞+关注
学习不迷路
