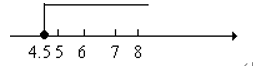
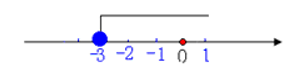
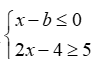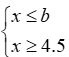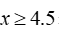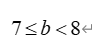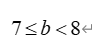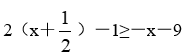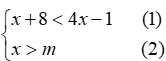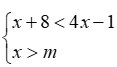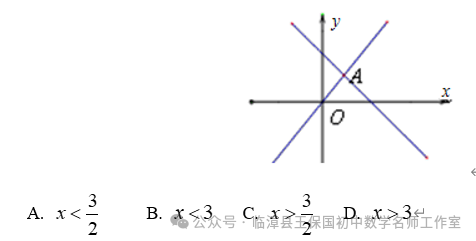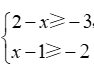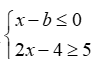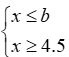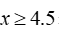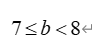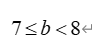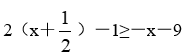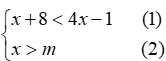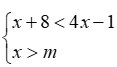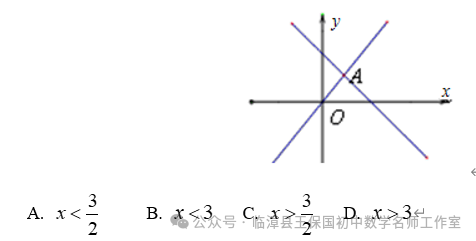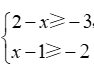教师简介:王保国,男,高级讲师,经常参与我县中小学听评课及课堂教学培训活动。2014年5月为《初中学科教师专业发展指导.数学》一书写作部分内容。临漳县拔尖人才,邯郸市优秀教师,河北省骨干教师,河北省特级教师,多次被评为邯郸市“一小时”培训优秀授课教师,多次被邯郸市教育局评为优秀辅导教师。邯郸市姜红梅初中数学名师工作室成员,临漳县初中数学名师工作室主持人。多年从事数学教学、研究及教师培训工作。《分类思想在课堂教学之中应用》《课堂小结的“六要”》等多篇论文在《中小学数学》与《小学教学参考》杂志上发表,2008年主持省级课题《提高教师新课程实施能力的途径与方式研究》等多个课题已结题,2020年主持的市规划课题《初中数学解题教学研究》于2024年7月已结题。且2013年1月主持的课题《初中数学课堂教学探究性学习研究》被邯郸市科协与教育局评为三等奖。在教师培训上,能从理论与实践两方面与教师交流,课堂教学效果好,如《核心素养下教学设计与策略》《核心素养下课堂教学》等受到教师好评。数形结合是数学解题中常用的思想方法之一。所谓数形结合,就是根据“数”与“形”之间的对应关系,通过数与形的相互转化来解决数学问题的思想。数形结合思想可以使数学领域中,某些抽象的问题直观化、具体化、生动化,能够变抽象思维为形象思维。在解有关不等式的问题时,有些问题需要我们借助图形来给出解答。解决此类问题时,要充分利用图形反馈的信息,或将文字信息反馈到图形上,做到有数思形,有形思数,顺利解决问题。解析:解决问题时,如果不结合图形,那么难度就会很大,所以为了顺利的解决问题,先化简原不等式组,得表示在数轴上如图,b的位置应是题意中告知的原不等式组有三个整数解,所以b必须包含5,6,7三个整数。所以b的取值范围是解析:首先,按照解一元一次不等式的步骤,求得不等式的解集;其次,把不等式的解集在数轴上表示出来,简单的,也可以不用数轴表示;最后,结合数轴确定不等式的特殊解。移项、合并同类项,得:2x+x≥-9,3x≥-9,结合数轴,知道原不等式的负整数解有-3,-2,-1一共三个。点拨:在数轴上表示不等式的解集时,要注意如下口诀:A. m=3 B.
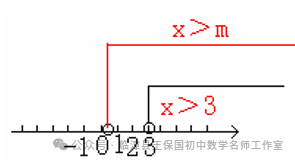
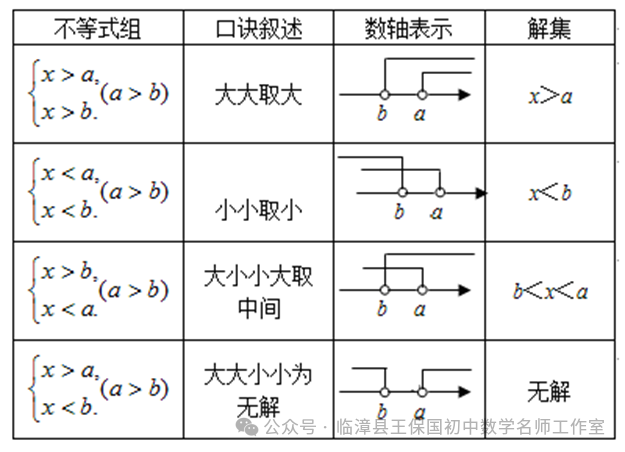
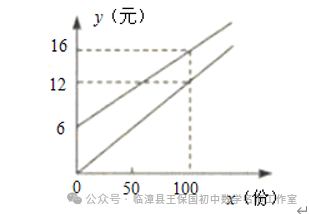
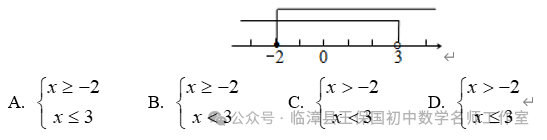
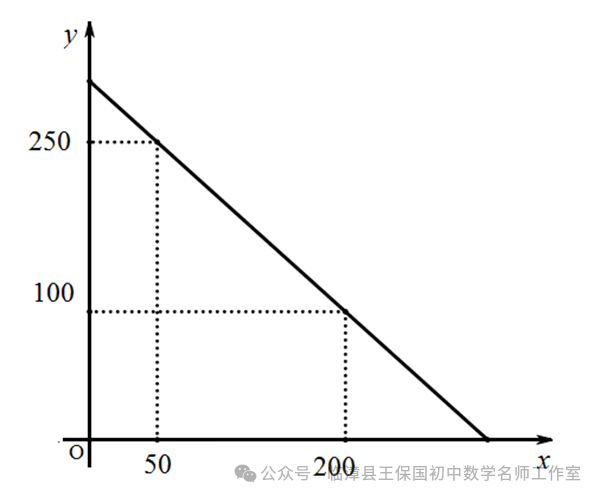
m≥3 C. m<3 D. m≤3解析:同学们先按照解不等式组的基本步骤,求得不等式组的解集,然后利用数轴,把解集在数轴上表示出来,因为不等式组有解,所以,在数轴上表示时,表示解集范围的两条射线,一定有公共部分。所以,同学们先在数轴上表示出解集的大致范围,然后根据范围的描述,就可以确定字母的范围。答案:因为,不等式(1)的解集是x>3;不等式(2)的解集是:x>m,所以,不等式组的解集在数轴上的大致范围,如图所示,仔细观察数轴,要想保证有公共部分,不等式的解集x>m的部分,必须在x>3的左边,因此,m的范围应该是:m≤3,所以,我们应该选择D。点拨:确定不等式组的解集一般有两种方法,即口诀法和数轴法,具体地可归纳如下表所示:例题1 (黔西)如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为( )解析:本题考查了一次函数与不等式之间的关系,解答本题的关键是求出m的值。要求不等式k1x<k2x+b的解集。即相当于比较两个一次函数值的大小,而从图象上可以直接捕捉到求解的信息。所以先利用函数y=2x求出点A的坐标,最后根据图象求出不等式的解集。点拨:1. 利用一次函数确定不等式解集的关键是能够正确的理解图象的意义,准确地从函数图象中捕捉数的信息。例题2 (山西)某校实行学案式教学,需印制若干份数学学案。印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要。两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示:(1)填空:甲种收费方式的函数关系式是 。乙种收费方式的函数关系式是 。(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算。解析:本题是一次函数与不等式的综合应用。从图象中确定两点的坐标进而确定一次函数的解析式,再根据两函数解析式建立不等式,通过解不等式求得最佳印刷方式。答案:(1)由题图可知甲种收费方式的函数关系为:y=0.1x+6,乙种收费方式的函数关系式为y=0.12x(2)由0.1x+6>0.12x,得x<300;由0.1x+6=0.12x,得x=300;由0.1x+6<0.12x,得x>300。由此可知:当100≤x<300时,选择乙种方式较合算;当x=300时,选择甲乙两种方式都可以;当300<x≤450时,选择甲种方式较合算。点拨:1. 两点法求一次函数的解析式,比较两种印刷方式的优劣需要借助于不等式进行。这一个知识点也是考试命题的热点。2. 有关不等式与函数结合的试题大致有两种情形:一是通过函数图象,利用不等式比较大小,二是利用不等式与函数结合确定最优方案和最值问题。2. (浙江)若实数a,b,c在数轴上对应位置如图所示,则下列不等式成立的是( )3. 某不等式组的解集在数轴上表示如图,则这个不等式组可能是( )12. (贵州)某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系如图所示。当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元。(3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元。问该超市有几种进货方案?哪种方案能使获利最大?最大获利为多少元?供稿:王保国 编辑:刘素萍 杨艳飞 编审:王保国
关注我,我会更精彩!

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至23467321@qq.com举报,一经查实,本站将立刻删除;如已特别标注为本站原创文章的,转载时请以链接形式注明文章出处,谢谢!